Point d'inflexion
À propos de la définition de point d’inflexion, et de plusieurs points de vues exposés ici :
http://www.les-mathematiques.net/phorum/read.php?4,690105,690220
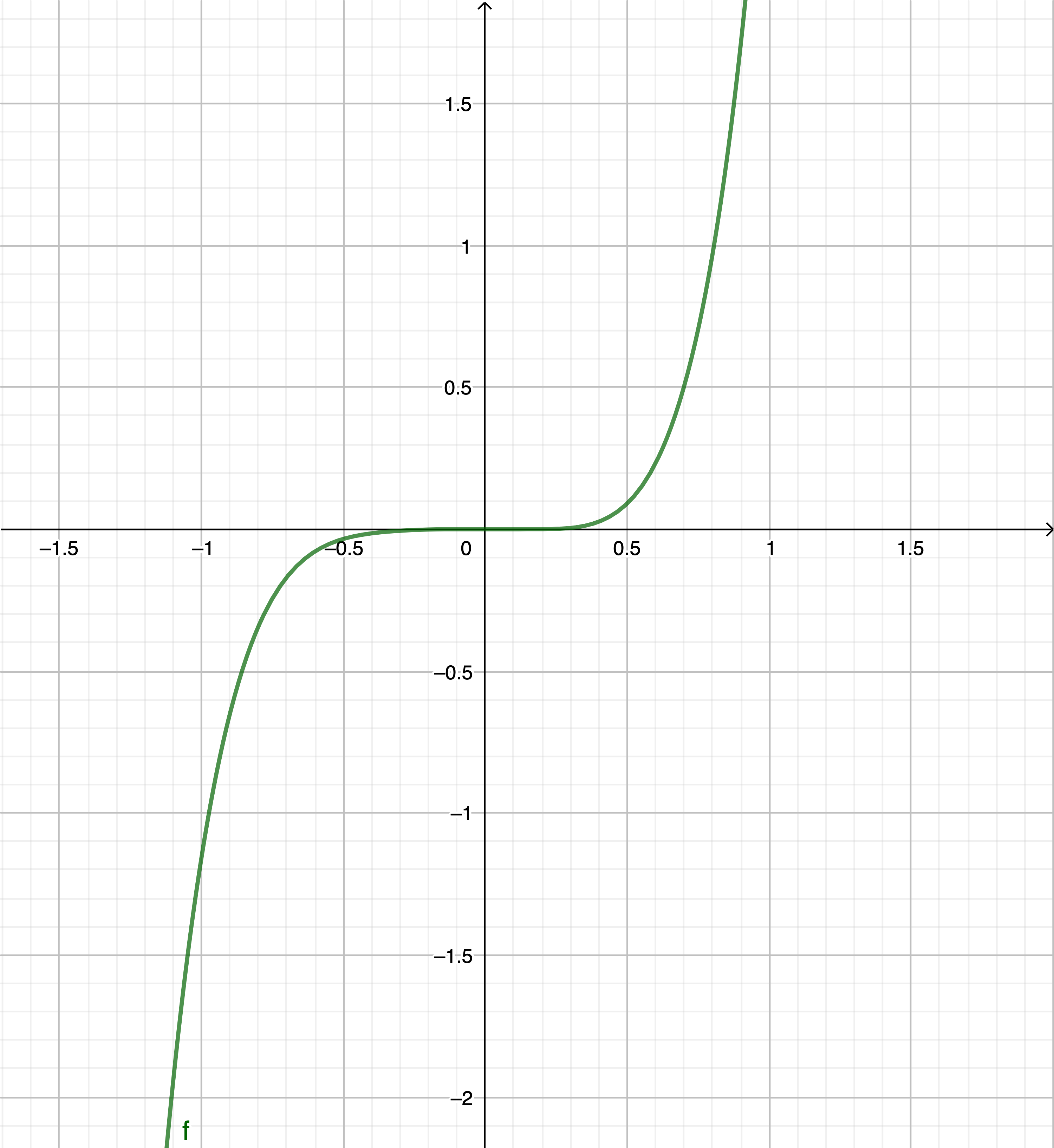
Ci-dessous, la représentation graphique de l’exemple
\(f(x)=x^5 \left ( \sin \left ( \dfrac{1}{x} \right ) + 2 \right)\) prolongée par continuité en \(0\) par \(f(0)=0\).
La courbe de \(f\) traverse sa tangente en \(0\), alors que \(f\) ne change pas de convexité en \(0\).
La courbe de \(f\) traverse sa tangente en \(0\) :
\(f\) est dérivable en \(0\) car \(\displaystyle \lim_{x \to 0} \dfrac{f(x)-f(0)}{x-0}=\lim_{x \to 0} x^4 \left ( \sin \left ( \dfrac{1}{x} \right ) + 2 \right) = 0\) et donc \(f'(0)=0\) et donc une équation de la tangente en \(0\) est \(y=0\)
La courbe de \(f\) traverse sa tangente en \(0\), car pour \(x>0\), \(f(x)>0\) et pour \(x<0\), \(f(x)<0\)
\(f\) ne change pas de convexité en \(0\) :
Pour \(x \neq 0\), \(f'(x)=5x^{4}\left(\sin\left(\dfrac{1}{x}\right)+2\right)-x^{3}\cos\left(\dfrac{1}{x}\right)\)
\(f'\) est dérivable en \(0\) car \(\displaystyle \lim_{x \to 0} \dfrac{f'(x)-f'(0)}{x-0}=\lim_{x \to 0} 5x^{3}\left(\sin\left(\dfrac{1}{x}\right)+2\right)-x^{2}\cos\left(\dfrac{1}{x}\right) = 0\) et donc \(f''(0)=0\)
Pour \(x \neq 0\), \(f''(x)=20x^{3}\left(\sin\left(\dfrac{1}{x}\right)+2\right)-8x^{2}\cos\left(\dfrac{1}{x}\right)-x\sin\left(\dfrac{1}{x}\right)\)
\(f''\) est continue en \(0\) s’annule en \(0\) et \(f''\) est continue sur \(\mathbb{R}\).
Pour \(k\in \mathbb{Z}\), \(f''\left(\dfrac{1}{k\pi}\right)=\dfrac{40}{k^{3}\pi^{3}}+(-1)^{k+1}\dfrac{8}{k^{2}\pi^{2}}\sim(-1)^{k+1}\dfrac{8}{k^{2}\pi^{2}}\)
donc \(f''\left(\dfrac{1}{k\pi}\right)\) est de même signe que \((-1)^{k+1}\) et donc \(f''(x)\) change de signe une infinité de fois dans tout intervalle ouvert contenant \(0\).
Ainsi \(f''(x)\) s’annule en \(0\), mais ne change pas de signe en \(0\).
et images avec différents zooms
inflexion1
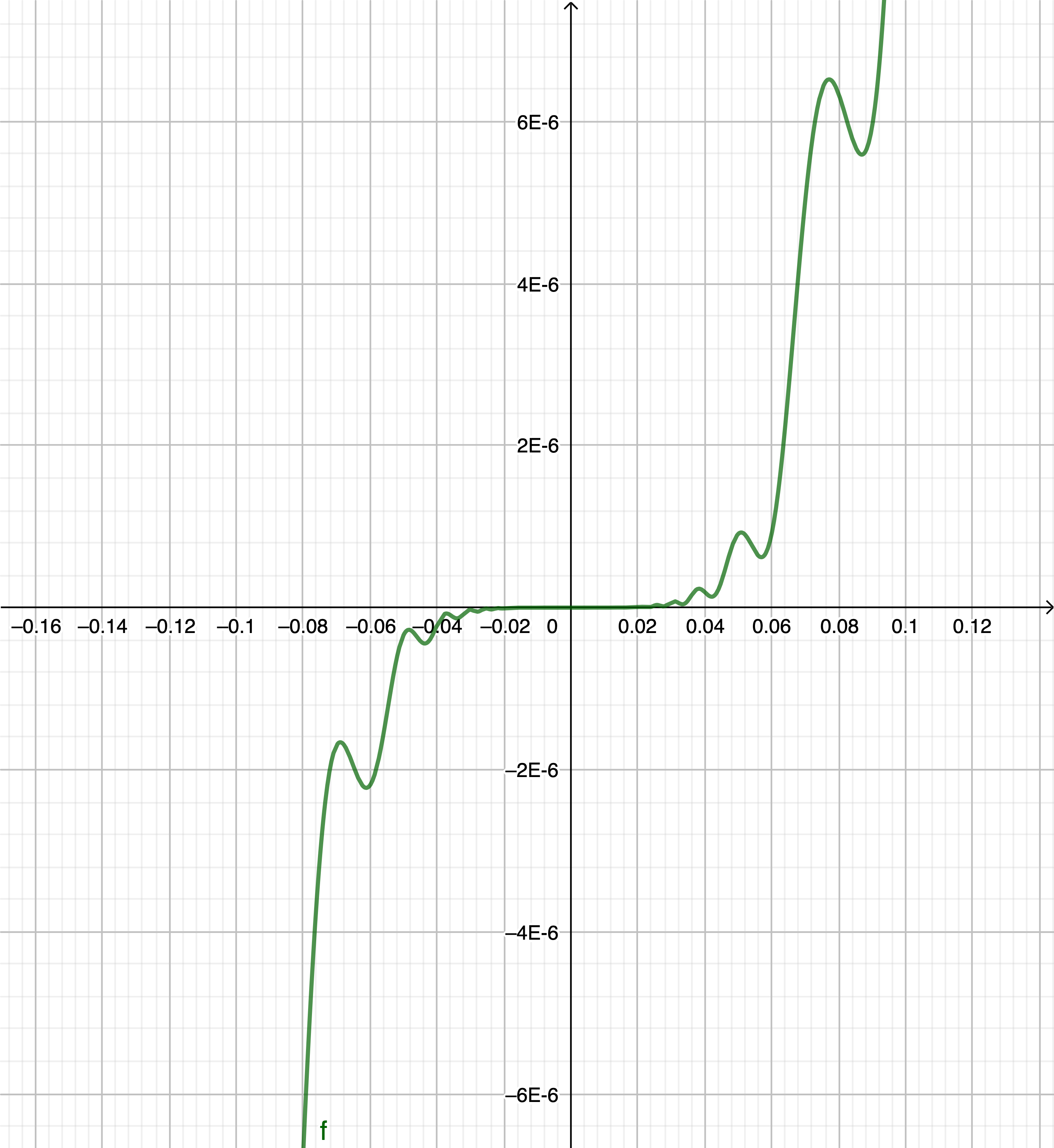
inflexion2
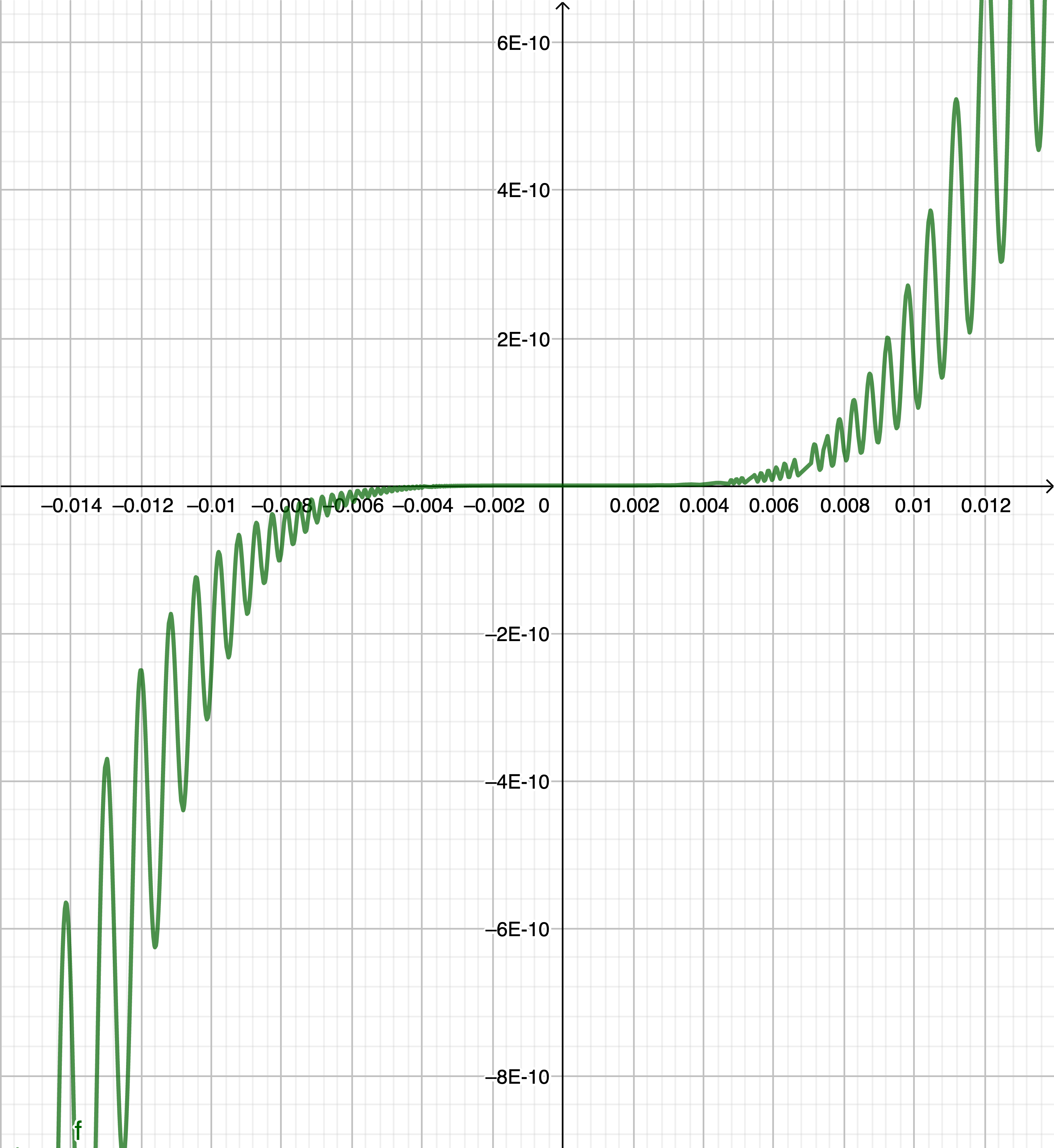
inflexion3